If you’re studying calculus or precalculus, you’ve likely encountered the term difference quotient. But what exactly is the difference quotient, how do you find it, and why is it important? In this article, we’ll break down everything you need to know — from the difference quotient formula to practical examples and step-by-step methods on how to solve difference quotient problems. Plus, we’ll mention some useful tools like the difference quotient calculator and Symbolab difference quotient solver to help you simplify your work.
What Is the Difference Quotient?
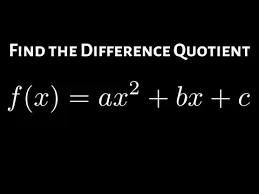
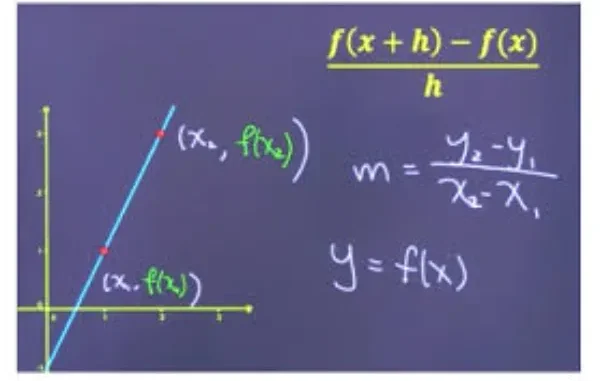
At its core, the difference quotient is a fundamental concept used to measure the average rate of change of a function over an interval. Simply put, it calculates the slope of the secant line between two points on the graph of a function.
In mathematical terms:
The difference quotient of a function f(x)f(x) is given by the expression:
f(x+h)−f(x)h\frac{f(x+h) – f(x)}{h}
where h≠0h \neq 0.
This formula represents the average rate of change of the function ff as the input changes from xx to x+hx + h.
Why Is the Difference Quotient Important?
The difference quotient is more than just a formula. It’s the foundation for understanding derivatives in calculus. When you take the limit of the difference quotient as hh approaches zero, you find the instantaneous rate of change — also known as the derivative of the function.
This is why mastering how to find the difference quotient and simplify it is a crucial skill for students progressing into calculus.
The Difference Quotient Formula Explained
Here’s a clear breakdown of the difference quotient formula:
Difference Quotient=f(x+h)−f(x)h\text{Difference Quotient} = \frac{f(x+h) – f(x)}{h}
- f(x)f(x) is the function evaluated at xx.
- f(x+h)f(x+h) is the function evaluated at x+hx+h.
- hh is the difference between the two inputs and must not be zero because division by zero is undefined.
The goal is often to find and simplify the difference quotient by substituting expressions for f(x)f(x) and f(x+h)f(x+h) into the formula and then simplifying the algebraic expression.
How to Find the Difference Quotient: Step-by-Step
Here’s a practical step-by-step guide on how to find the difference quotient for any function:
- Write down the function f(x)f(x).
Example: f(x)=3×2+2x−5f(x) = 3x^2 + 2x – 5 - Calculate f(x+h)f(x+h) by replacing every xx in f(x)f(x) with (x+h)(x+h).
For the example:
f(x+h)=3(x+h)2+2(x+h)−5f(x+h) = 3(x+h)^2 + 2(x+h) – 5
- Expand f(x+h)f(x+h) using algebraic rules.
f(x+h)=3(x2+2xh+h2)+2x+2h−5=3×2+6xh+3h2+2x+2h−5f(x+h) = 3(x^2 + 2xh + h^2) + 2x + 2h – 5 = 3x^2 + 6xh + 3h^2 + 2x + 2h – 5
- Substitute f(x+h)f(x+h) and f(x)f(x) into the difference quotient formula.
f(x+h)−f(x)h=(3×2+6xh+3h2+2x+2h−5)−(3×2+2x−5)h\frac{f(x+h) – f(x)}{h} = \frac{(3x^2 + 6xh + 3h^2 + 2x + 2h – 5) – (3x^2 + 2x – 5)}{h}
- Simplify the numerator by canceling out like terms.
=6xh+3h2+2hh= \frac{6xh + 3h^2 + 2h}{h}
- Factor out hh in the numerator and simplify the fraction.
=h(6x+3h+2)h=6x+3h+2= \frac{h(6x + 3h + 2)}{h} = 6x + 3h + 2
- State the simplified difference quotient.
6x+3h+26x + 3h + 2
Difference Quotient Examples
Let’s look at a few common examples to illustrate how to solve difference quotient problems.
Example 1: Linear Function
f(x)=5x−7f(x) = 5x – 7
- Calculate f(x+h)=5(x+h)−7=5x+5h−7f(x+h) = 5(x+h) – 7 = 5x + 5h – 7
- Substitute into the formula:
(5x+5h−7)−(5x−7)h=5hh=5\frac{(5x + 5h – 7) – (5x – 7)}{h} = \frac{5h}{h} = 5
The difference quotient simplifies to 5, which is the slope of the linear function.
Example 2: Quadratic Function
f(x)=x2f(x) = x^2
- f(x+h)=(x+h)2=x2+2xh+h2f(x+h) = (x+h)^2 = x^2 + 2xh + h^2
- Substitute into formula:
x2+2xh+h2−x2h=2xh+h2h=2x+h\frac{x^2 + 2xh + h^2 – x^2}{h} = \frac{2xh + h^2}{h} = 2x + h
How to Solve Difference Quotient Using a Calculator
If you want to speed up the process, you can use a difference quotient calculator. Many online calculators, including Symbolab difference quotient, allow you to input the function and the value of xx and hh, and the tool automatically computes and simplifies the expression.
Just search for “difference quotient calculator” or use the Symbolab difference quotient solver for step-by-step explanations and graphing features.
Tips to Find and Simplify the Difference Quotient
- Always expand and simplify f(x+h)f(x+h) carefully.
- Cancel out identical terms in f(x+h)−f(x)f(x+h) – f(x) to avoid unnecessary complexity.
- Factor hh in the numerator to simplify the expression by canceling with the denominator.
- Remember h≠0h \neq 0 — if the expression includes hh after simplification, don’t substitute h=0h = 0 yet (this comes later when finding derivatives).
Frequently Asked Questions About Difference Quotient
What is the difference quotient used for?
It measures the average rate of change of a function over an interval and serves as the foundation for derivatives.
How do I find the difference quotient for any function?
Calculate f(x+h)f(x+h), subtract f(x)f(x), divide by hh, then simplify the result.
Can I use a calculator to solve difference quotient problems?
Yes, online tools like Symbolab difference quotient solver or other difference quotient calculators can help.
Conclusion
The difference quotient is a crucial stepping stone toward understanding calculus and derivatives. By mastering how to find the difference quotient, applying the difference quotient formula, and practicing with various examples, you’ll be well-equipped to tackle more advanced math problems.
Whether you prefer manual algebraic work or using a difference quotient calculator, understanding the principles behind the difference quotient is key to success in your math studies.
If you want a quick start, try entering your function into a Symbolab difference quotient calculator or any trusted online tool to see step-by-step solutions and build confidence.
Leave a Reply